Additional Exercises

1:	Plot the following three curves on a single plot and a multiple plots (using the subplot command): 2 cos(t), sin(t), and cos(t)+sin(t). Use a time period such that two or three peaks occur for each curve. Use solid, dashed, and + symbols for the different curves. Use roughly 25–50 points for each curve.
2:	a. Calculate the rank, determinant, and matrix inverse of the following matrices (use help rank, help det, and help inv):
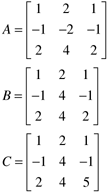
3:	Find C·C–1 where
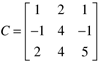
4:	Calculate xTx, and calculate xxT where
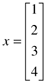
5:	Find the eigenvalues of the matrix
6:	Find the solutions to the equation f(x) = 3x3 + x2 + 5x-6 = 0. Use roots and fzero.
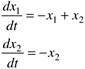
7:	Integrate the equations, from t = 0 to t = 5 with the initial condition x1(0) = x2(0) = 1. Use ode45 (Module 3) and plot your results.