17.4 Notation

A	Jacobian	state space—relates states to the state derivatives
B	input matrix	state space—relates inputs to state derivatives
C	output matrix	state space—relates states to outputs
D		state space—direct transmittance from inputs to outputs
e	error	setpoint—measured process output
l	load (disturbance) input
p	pole	roots of the denominator polynomial of gp(s); equal to the eigenvalues of A
r	setpoint	desired value of the output
s	Laplace domain variable	when used in frequency-response techniques, set s = jw
x	state variable
y	output variable	measured output (also known as the controlled variable or process variable)
u	manipulated input	also known as the controller output
z	zero	roots of the numerator polynomial of gp(s) equal to the poles of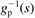
gp(s)	process transfer function	y(s) = gp(s) u(s) gp(s) = C(sI – A)-1B+D
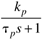
	first-order transfer function, gp(s)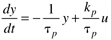
gc(s)	controller transfer function
gd(s)	disturbance transfer function
gm(s)	measurement transfer function
gv(s)	valve transfer function
kp	process gain	change in output/change in input
tp	process time constant	first-order system time constant
q	process time delay
z	damping factor	used for unfactored second-order systems
kc	proportional gain	PID controller tuning parameter
tI	integral time constant	PID controller tuning parameter
tD	derivative time constant	PID controller tuning parameter
tF	filter time constant
~	indicates model	superscript
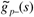
	"good stuff" portion of process model	inverse is used for internal model controller
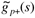
	"bad stuff" portion of process model	contains time-delays and RHP zeros
q(s)	internal model controller
f(s)	IMC filter	used to make q(s) physically realizable (proper)
l	filter factor, closed-loop time constant	tuning parameter for internal model controllers
l	eigenvalue	roots of det(lI – A)
lij	relative gain	relative gain between output i and input j
CLTF	closed-loop transfer function
GM	gain margin	indication of "gain uncertainty" that can be tolerated
IMC	internal model control	can be either implemented in the IMC structure or rearranged to "standard feedback form" to design a PID controller (IMC-based PID)
MIMO	multi-input, multi-output
MPC	model predictive control	optimization of control moves over a future prediction horizon
MVSISO	multivariable SISO	"decentralized control"—consists of several SISO controllers
NMP	nonminimum phase	a NMP process has right-half-plane zeros and/or time delays
PM	phase margin	indication of "phase uncertainty" that can be tolerated (usually used to find the amount of time delay that can be tolerated)
PID	proportional-integral-derivative (ideal)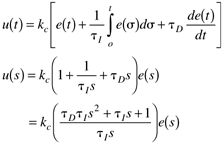
PID	proportional-integral-derivative (real)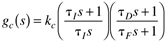
RGA	relative gain array	used for variable pairing and interaction analysis
RHP	right half-plane	right-half-plane zeros have inverse response
SISO	single input–single output
SVD	singular value decomposition	indicator of directional sensitivity