9.5 Summary of IMC-Based PID Controller Design for Stable Processes
We have shown several examples where the IMC design procedure could be used to develop an equivalent PID-type control law. For stable processes with no time delay, the IMC-based PID procedure gives exactly the same feedback performance as does IMC. For stable processes with a time delay, the IMC-based PID procedure will not give exactly the same performance as IMC, because a Padé approximation for dead time is used in the controller design.
We want this following point to be clear to the reader. For process transfer functions without time delays, the IMC-based PID controller will yield exactly the same performance as does IMC. This will occur if no approximation has to be made in the process model to find a feedback form that is equivalent to PID. If an approximation (such as Padé) is made in the IMC-based PID strategy, and this approximation is not made in the IMC strategy, then the performance will not be the same.
It should also be noted that although the standard IMC filter form, f(s) = 1/(ls + 1)n, leads to good setpoint tracking, it generally does not lead to good rejection of disturbances that have dynamics similar to the process transfer function. It is generally better to use a filter of the form f(s) = (gs + 1)/(ls + 1)n.
Table 9-1 provides a summary of the PID tuning parameters for systems without a time delay. Table 9-2 summarizes the PID tuning parameters for stable processes with a time delay. Notice that there are minimum recommended values for l shown, since there is inherent model uncertainty due to the Padé approximation. Selecting l near this value will put the closed-loop system on the edge of stability, so most often your initial tuning values for l will be significantly larger than these minimum values.
Table 9-1. Ideal PID Tuning Parameters for Open-Loop Stable and Integrating Processes.|
A | 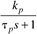
| 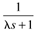
| 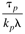
| tp | | | B | 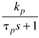
| 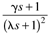
| 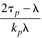
| 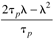
| | | C | 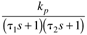
| 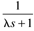
| 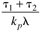
| t1 + t2 | 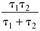
| | D | 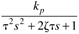
| 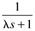
| 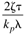
| 2zt | 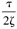
| | E. | 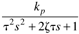
| 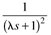
| 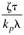
| 2zt | 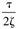
| 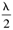
| F[c], | 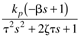
| 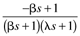
| 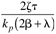
| 2zt | 
| 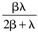
| G[d] | 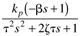
| 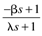
| 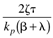
| 2zt | 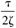
| | H | 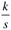
| 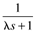
| 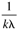
| | | | I | 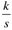
| 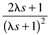
| 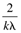
| 2l | | | J | 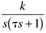
| 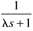
| 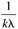
| | t | | K[e] | 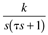
| 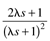
| 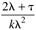
| 2l + t | 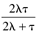
| |
Table 9-2. PID Tuning Parameters for Stable Time-Delay Processes|
A | 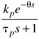
| 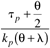
| 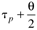
| 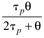
| 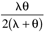
| 1 | B | 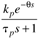
| 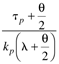
| 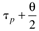
| 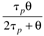
| | 2 | C | 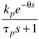
| 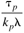
| tp | | | 3 | D | 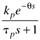
| 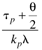
| 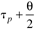
| | | 4 | E | 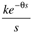
| 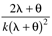
| 2l + q | | | 5 | F | 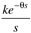
| 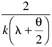
| 2l + q | 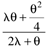
| | 6 | G | ke–qs | 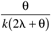
| 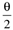
| | | 7 | H | ke–qs | 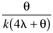
| 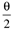
| 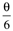
| 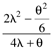
| 8 |
|