Additional Exercises

1:	Consider the van de Vusse reactor, which has the following state space model at the nonminimum-phase operating point: where Find the sample time that will bring the zero (discrete time) that is outside the unit circle to the unit circle. Compare the discrete-step response for this sample time with the continuous system step response.
2:	Consider the first-order process (where the time unit is minutes and the gain is °C/%) If discretized with a sample time of 1 minute, the discrete-time model is Design continuous and discrete IMC controllers and compare performances on a unit step setpoint change. Study various values of the IMC tuning parameter, l.
3:	Consider the second-order process (where the time unit is minutes and the gain is %/%) If discretized with a sample time of 3 minutes, the discrete-time model is Consider factorizations for the discrete IMC design when (a) the negative zero inside is not factored out, and (b) the negative zero inside the unit circle is factored out. Compare the two digital controllers and continuous IMC performances on a unit step setpoint change. Study various values of the IMC tuning parameter, l.
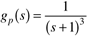
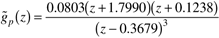
4:	Consider the third-order process (where the time unit is minutes, and the gain is %/%) which has no zeros (that is, it is minimum phase). If the model is perfect, we know that a continuous-time controller can be tuned arbitrarily tightly. If the continuous model is discretized with a sample time of 1 minute, the discrete-time model (in factored form) is Notice that one of the process zeros is at –1.7790 (outside the unit circle); if the inverse of the model is used for controller design, an unstable controller results. It is interesting that the continuous-time model has no RHP zero, yet the discretized model has a zero outside the unit circle. Consider factorizations for the discrete IMC design when (a) the zero at –1.7990 is not factored out, and (b) the zero at –1.7990 is factored out. Compare the two digital controllers and continuous IMC performances on a unit step setpoint change. Study various values of the IMC tuning parameter, l.